Here, I outline my influences, attempt a critical hindsight-laden review of past efforts.
My project began as a different take on the early (1991) work of Peter Rowlands[2], with an attempt to deduce the seemingly missing combinatorial trivector states from the three dualities. Rowlands named four out of a possible eight states. This is how my project earned its name, "Pieces of Eight".
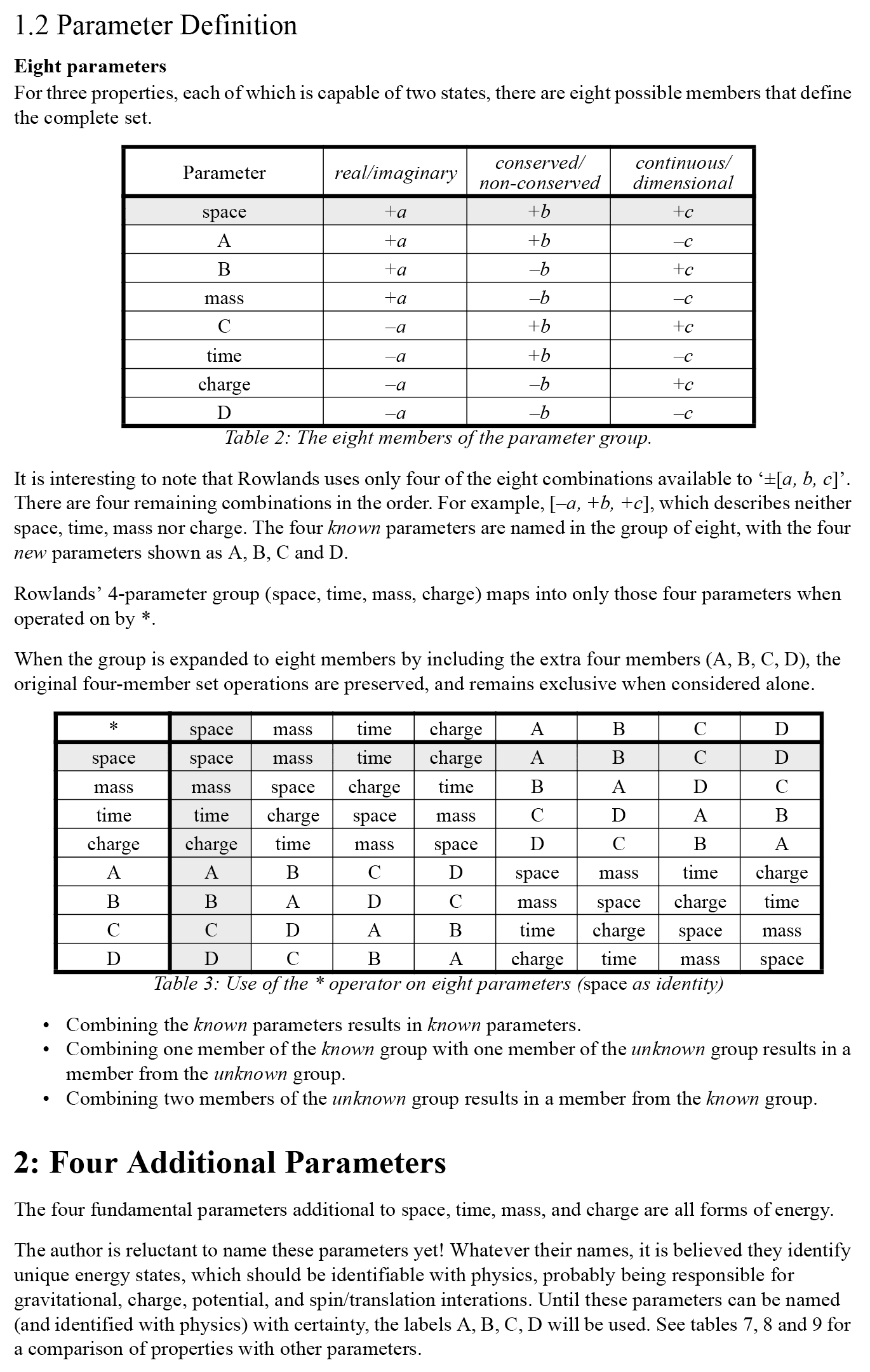
Fig.1: Eight parameters.[4]
I identified the dual algebras of the vacuum, and its structure. This conservation duality is the single b axis that I use in current work.
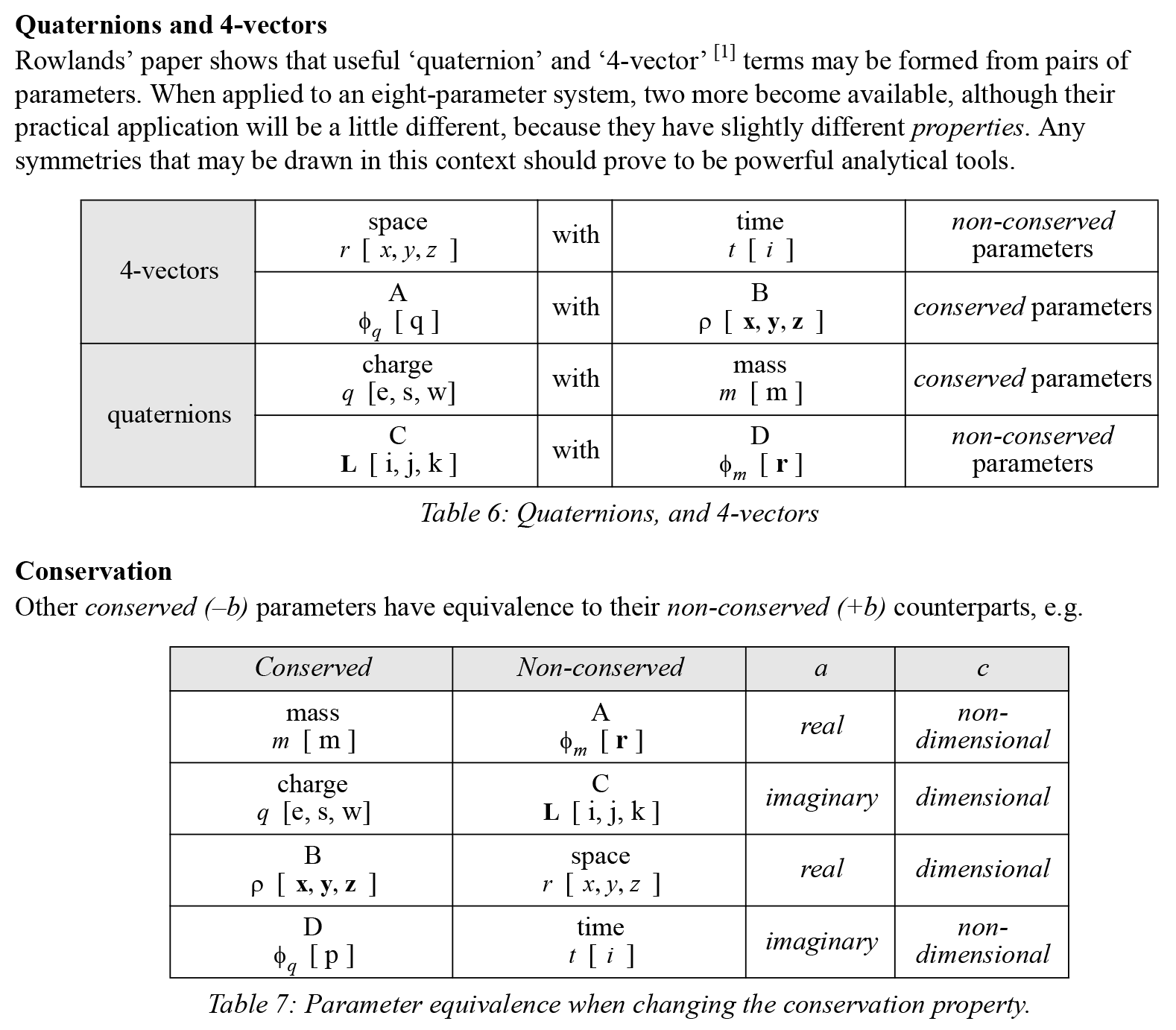
Fig.2: Useful mathematical structures, and the vacuum duality (two others not shown here).[4]
At ANPA[4] I attempted to frame the question and approach the answers, along with a way of forming simple closed (singlet-like) systems using discrete phase operators. The eight items were imposed into Klein-4-like groups (D2, using three orthogonal discrete reflection symmetries), such that a chain of operations returned to zero or the identity element.
First, I encoded the properties (implying symmetries and changes) of each parameter as a number, 0 to 7, like a bitwise Kronecker delta function.
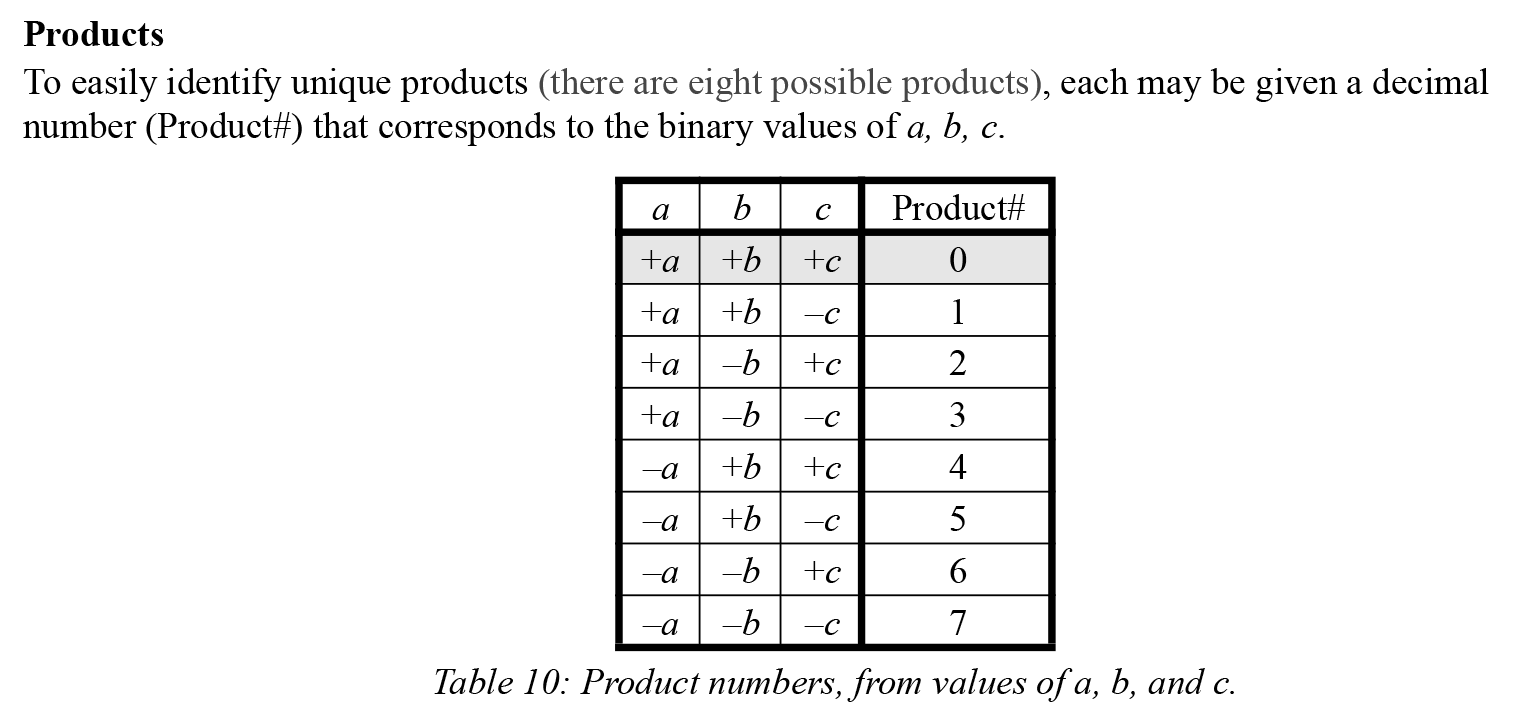
Fig.2: Encoded operators.[4]
Next, they were combined into pairs of parameters, and these were likewise given an equivalent product number. Where two identical product numbers are combined, the resulting product is zero.
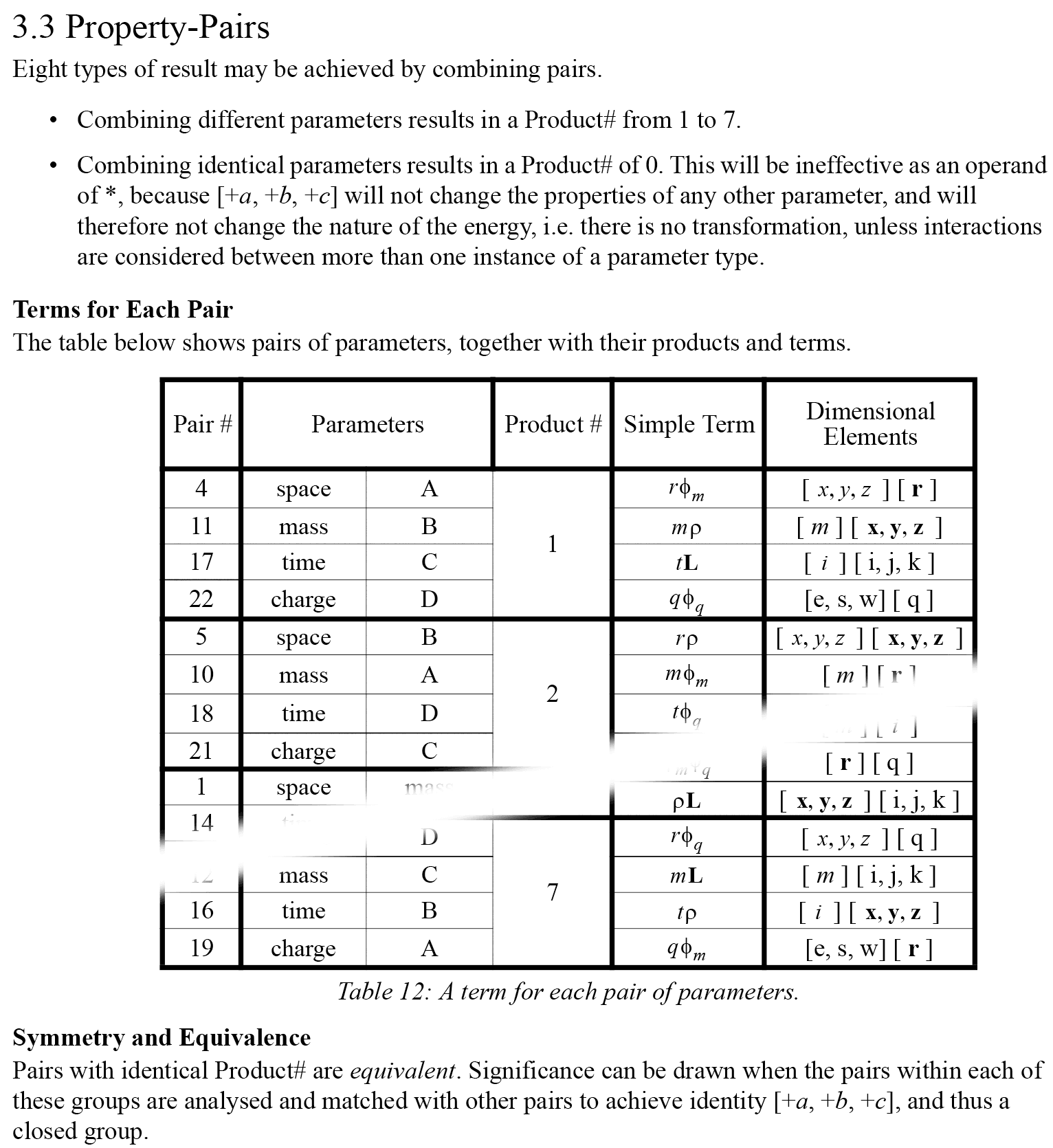
Fig.3: Equivalent pairs, combining to zero (some omitted for brevity).[4]
It was suggested that reality is a sequence of events, deviating from identity as two parts, one the conjugate of the other, and both with different algebraic structure, and not necessarily closing at the same event.
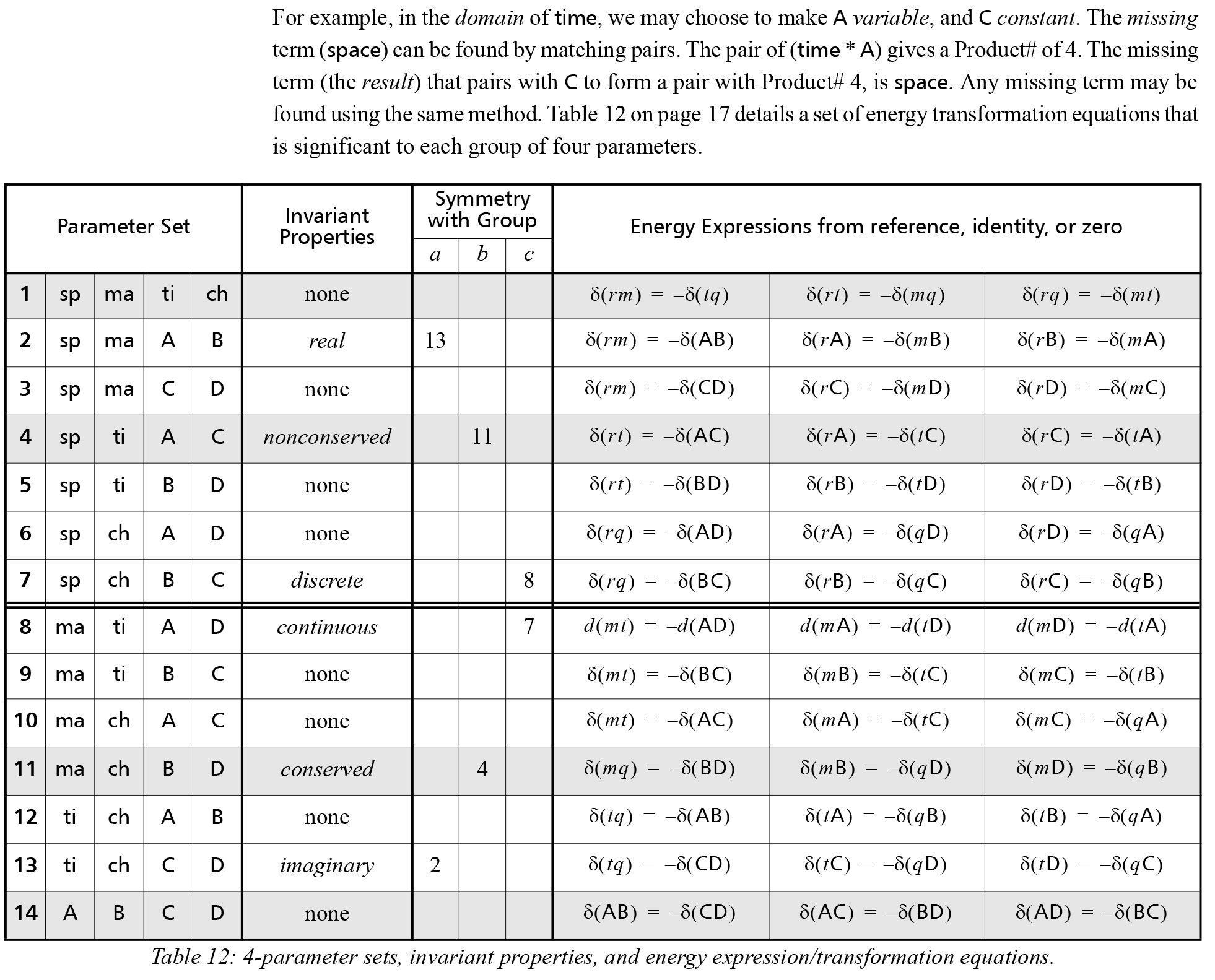
Fig.4: Divergent expressions (duals).[4]
This initial effort had only limited success for many reasons: the states themselves defied definition because the context and language to describe them was not available, the common fundamental abstractions used in physics failed to slot neatly into the available places, it lacked a model, and did not reveal the ontology of matter.
However, it was successful as an exercise in algebra, and provided some brief novelty interest. Perhaps the most useful 'discoveries' to emerge from that initial development were (a) the proposition that just one algebraic basis axis was needed to distinguish a fermionic particle from a bosonic wave state, an idea at the heart of my current work; and (b) that matter has counterpart vacuum elements, equivalent in origin, but not identical in structure.
In a retrospective analysis, the following extract is a significant prediction of the mathematical power of the algebraic approach:
It is possible to imagine a topology (e.g. a pairing, or ‘chained-ring’ in a group) of states that mirror each others’ energy distributions in different parameters, ... merely the result of cycling or mirroring the members of the 8-parameter system ... They are just different expressions of the dual viewpoints onto the same universe. These abstract views need to be transformed to relate to my space (and time).
The system of eight parameters has four groups which are just as valid as the conventional group (space, time, mass, and charge) as a reference. Principles of symmetry and transformation may be used (with care!) to alter the context of the energy, if an alternative reference is needed. It should be possible to use any group as a reference to describe all interactions, but this should not be necessary if the correct terms are used to begin with.
After these relatively unproductive lines of enquiry, the 2006 work took those three important duals of physics, applied them directly as a phase space (extending the previous ‘discrete closure’ into a continuous space), and created a minimal model for physicality while including some basic fundamental requirements. The discrete reflection operations of D2 duals were changed to be the continuous rotation operators of C2, operating cyclicly over ±1 continuous values, interpolating over the components of the Clifford algebras.
In hindsight, I view the 2006 work as a stepping stone to better work, setting the stage for answering questions of physicality, and placing emphasis on just one axis of the three-basis model, so setting the agenda for a leaner model.
Fig.5: continuous waves, states, closure, factorisation, 2006. [7]
In 2008, I presented the ideas more clearly, showing a deterministic network of fermions and bosons, exclusion, an origin for mass-energy, and its modulation effect as a phase operator on other bosons.
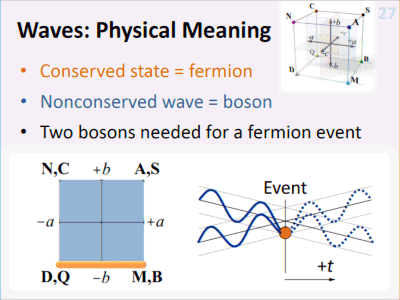
Fig.6: Physicality of a fermion from bosons, 2008. [10]
Fig.7: Definition of mass-energy, 2008. [10]
Further, I elaborated on the ways that combinations of the elements from the 8-parameter (16-dimensional expansion) algebra necessarily privileges at least two of them, to imply a symmetry breaking and physical context, and that there were many other ways of privileging the algebra, to identify different contexts:
Fig.8: Existing algebras from 3×D2, 2008. [10]
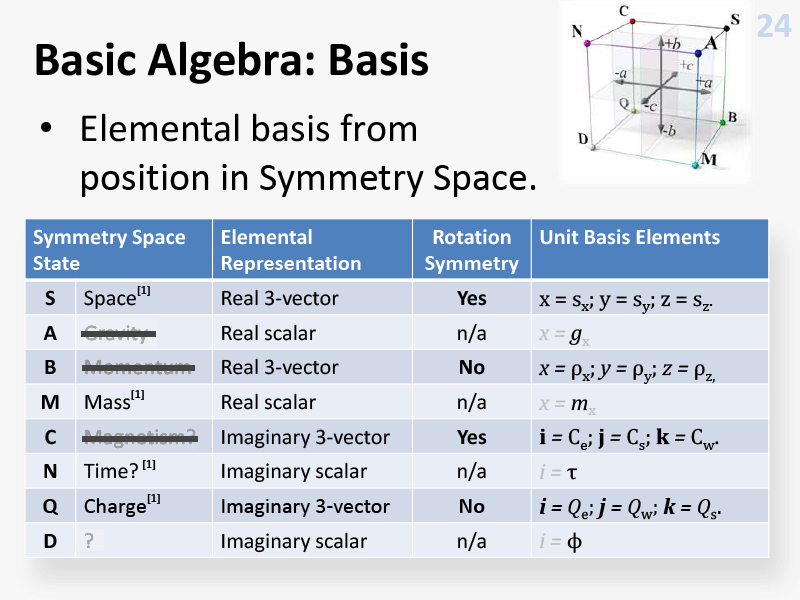
Fig.9: 16 unit basis elements, 2008. [10]
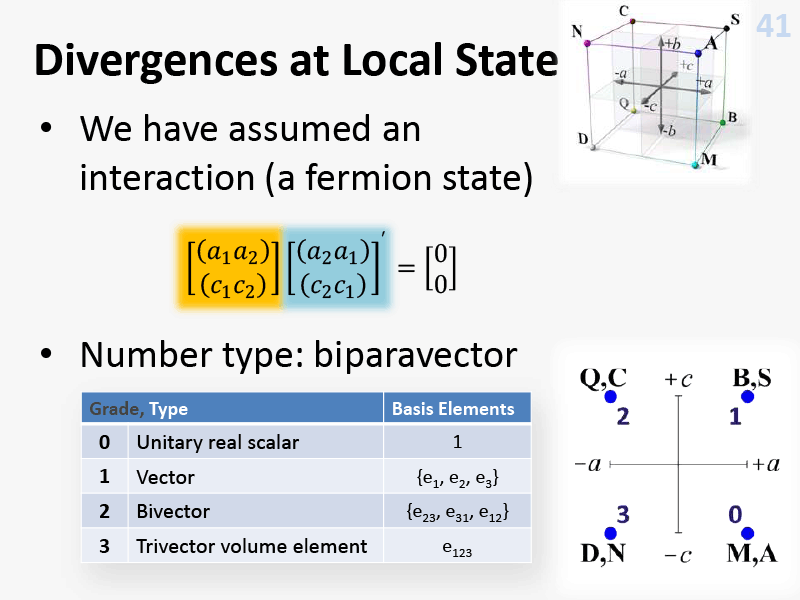
Fig.10: Splitting zero-product, 2008. [10]
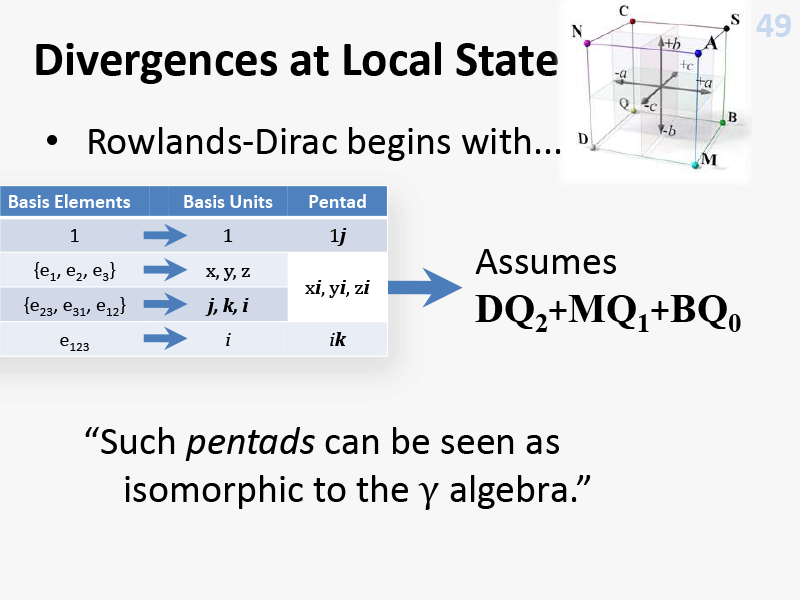
Fig.11: Algebraic origin of Dirac model, 2008. [10]
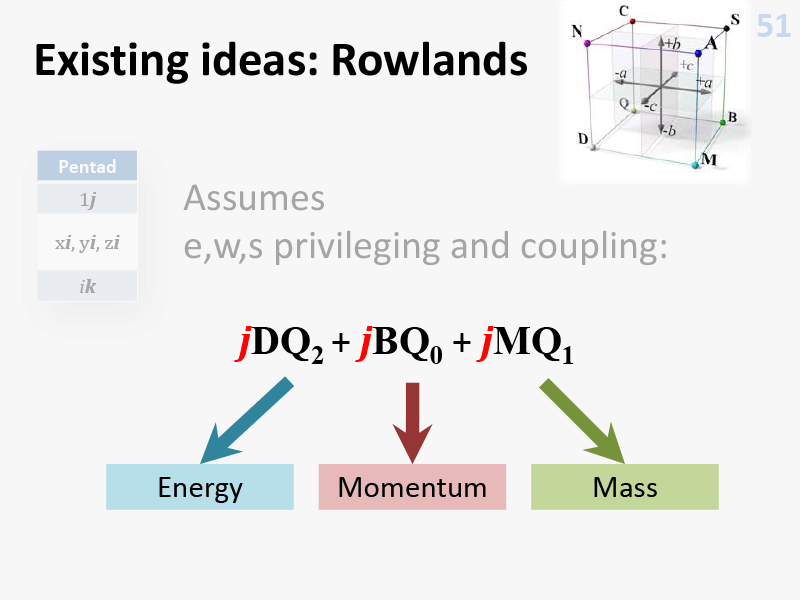
Fig.12: emergent quantities after privileging, 2008. [10]
In private communications with Rowlands [February 2009], the four extra (anti-)terms again defied satisfactory definition, but it was noted that they could exist as conjugate aspects to the named terms, and the argument can be repositioned as epistemological rather than solely ontological: they are components of the nilpotent formulation, rather than physical components in their own right. This means that the states may be re-encoded by rotations, given the appropriate algebraic framework.
Overall though, many aspects of both bodies of work (Rowlands, Valentine) agree with a broad overlap, but have been reached via different approaches and reasoning. I believe this bodes well for the foundational ideas expressed by Rowlands (pre-1991), from the perspective of authors from different backgrounds being able to access similar conclusions by different logical processes.
I have since paid less attention to the complete expansion of the geometric algebra structure (real, imaginary) × (non-dimensional, 3-dimensional) × (conserved, nonconserved), to concentrate on a means to reproduce physicality using just one axis, the (conserved, nonconserved) or b axis in the 1991 work.
The single algebraic basis for states and waves is fruitful, allowing physicality to 'emerge' from a simple process of phase propagation. I've written extensively on 'entity' and 'exclusion' to demonstrate the rigour of the physical basis, but feel this is of minority philosophical interest, so I prioritised other works at the time.
Instead, my work focused on the ontology of matter and energy, identifying matter and vacuum as different phases of the same propagating waves. My vacuum is not universally isotropic, allowing different conditions and behaviour of matter and energy in different regions of the universe. I have a good relativistic description of quantum processes, and can identify terms of the conventional wavefunction as statistics of my foundational model. [more...]
I judged that the foundation paper was good enough to start writing some specialized works, choosing subjects where the currently-accepted best answers are non-trivial.
These three works were consolidated into a more coherent report, the 2014 paper, "Minimal Deterministic Physicality Applied to Cosmology".
Since 2014, I've expanded this Wiki to describe some known physical phenomena in terms of my foundations. I also started working on simulation software that generates these phenomena from simple configurations.
After a ten year break, I created a simulation engine with most of the functionality I need, and started on a web interface for research and demonstrations. I wrote the 2024 paper as an interim report on the simulator results and design, but I saw it as an excellent opportunity to explain what the mechanism does. The paper contains no fundamental changes to the mechanism outlined in earlier papers, but it expands deeper into emergent properties that have meaning for high-energy physics, exploring weak interaction, fermion generations, and reconciling more content with the Standard Model. I foresee lots of communication work to express the deterministic approach in terms of field theory, so practitioners have a basis for tracing concepts to my foundations.
The formulation proposed by Rowlands[5] builds its algebra from his nilpotent universal computational rewrite system, which uses a simple symbol as both a state and an operator, that can either conserve itself or generate a new symbol. Meanings for the next new symbols are also proposed, which act as ‘complexify’ and ‘dimensionalize’ operators. In common with a group inverse operation, re-application of the latter two symbols reverses their respective effects, and re-use of the first symbol instantiates new entities.
Although I've not assumed any ‘creation roots’ from which a universe may emerge from self-rewrite, I've instead deduced a physical model and phase space from the requirement to resolve all other interacting objects uniquely from any given object. This resulted in my use of unique relative phases for resolved boson waves (like their e–i(Et – p.r) to close the nilpotent), and our use of an absolute reference phase –b, to give ‘wave phase’ an absolute meaning and physical symmetry, and also to provide a trivial physical structural means for fermions to re-instantiate themselves in causal sequence from the minimal amount of information encoded in the bosons. I gave the Rowlands symbolic abstraction an underlying physical context in the form of my matter network.
The key difference in our approaches, is that I've concentrated on the (self-) process and model to derive qualitative results from the physical structure of matter, using only one of the fundamental dualities, and have only outlined the full geometric algebra of a fermion event, achievable from {a, c}, leaving its detail (e.g. groups, algebraic equivalence, spin formulation) to others [Clifford, Hamilton, Lie, Hestenes[3], Rowlands[8], Almeida[9]] as ‘standard texts’. In comparison, Rowlands has specialized on the algebraic structure of what I call the ‘fermion event’, using the nilpotent formulation, to give quantitative results and expression in many scientific disciplines. I think the most noteworthy point of the rewrite system is the use of three the dualities to create a full algebra (and by “full”, I mean that it retains the information that many other physical theories accidentally discard by omission); my {b} duality find expression as a dual algebra for the vacuum in their work, providing an immediately-accessible conjugation from conserved sources to their respective nonconserved bosons, fields, and quantum potentials, to form a full picture of possible states that an entity might assume.
Likewise, my physicality has analogues with Peter Marcer's notion[13] of states relative to an [absolute] reference wave. I derive the observables from the {a, c} elements of the APS, rather than from the {b} reference wave, because the {b} wave cannot itself be measured (in common with Marcer's method), because it determines the points at which fermion events may form, which are the only points at which reality can be measured; we cannot arbitrarily measure bosons where {b} phases do not meet the criteria required for a fermion event.
Although different language is used in respective works, our interpretations on degeneracy and coherence as phase offset from the reference wave state –b are similar. The idea of co-homology is the same in both cases; any differences are solely because of our respective interpretations of matter constitution, rather than any difference in our respective derivations of the principles and self-processes of quantum computation.
