Entanglement
Radiation
Our mechanism describes a fermion as two bosons that collapse at a unique point. These bosons are continuously oscillating, so spend no time at the fermion; they radiate immediately from that point. Nothing is left behind; the entire fermion is radiated away as bosons, in the same shell.
This radiation is fundamentally scalar (defined in one dimension), and has equivalent propagation in phase, time, and space. In 3D space the boson takes the shape of a sphere shell of zero width, expanding at light speed, and oscillating at a rate of one cycle per Planck length.
Criteria for entanglement
This gives us the key ingredients for entanglement: a mix of uncollapsed waves occupying exactly the same space or surface; they are spatially indistinguishable from each other.
We say that two entities are entangled if they originated from the same event. Because all waves propagate at the same speed, there can be no change in the phase difference between entangled entities. Spatial differences cannot emerge to create any phase difference unless there is external input to break any symmetry that exists.
In our mechanism, there is an abundance of entanglement: it is an intrinsic aspect of every fermion event, because at least four waves are emitted from every fermion event, all entangled.
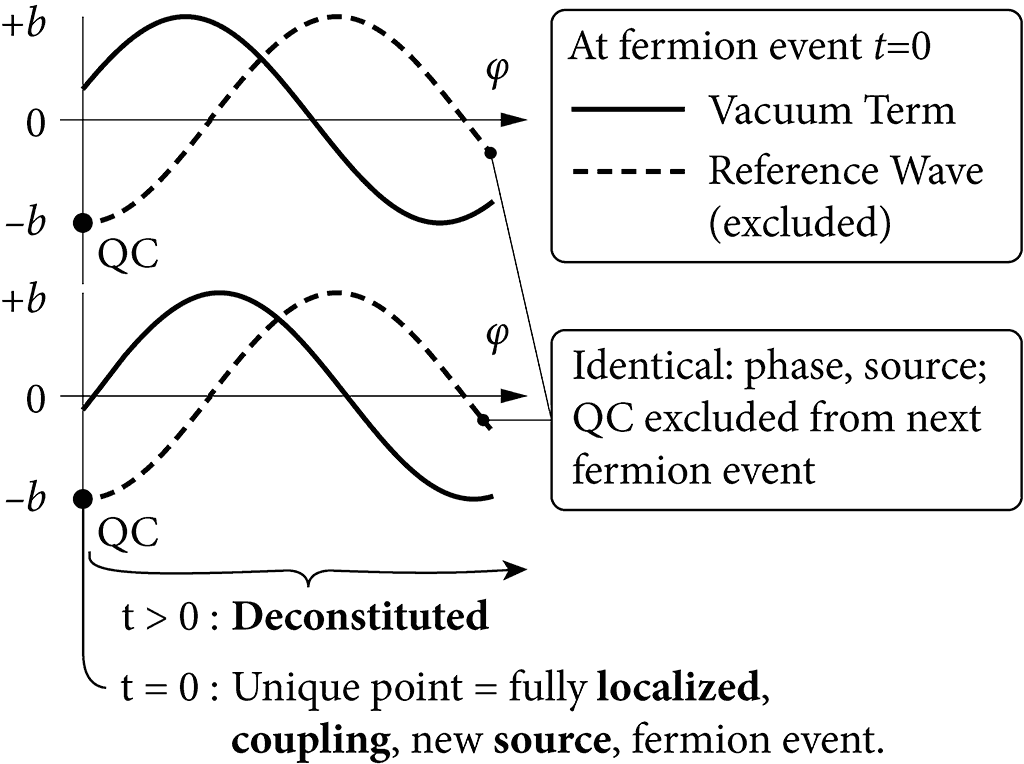
Fig.1: Fermion Event.
Collapse
Exclusion
Where the waves have exactly the same phase — which also happens in every fermion event — those waves are excluded from forming fermions, as shown by the dashed waves emerging from fermion A in fig.2.
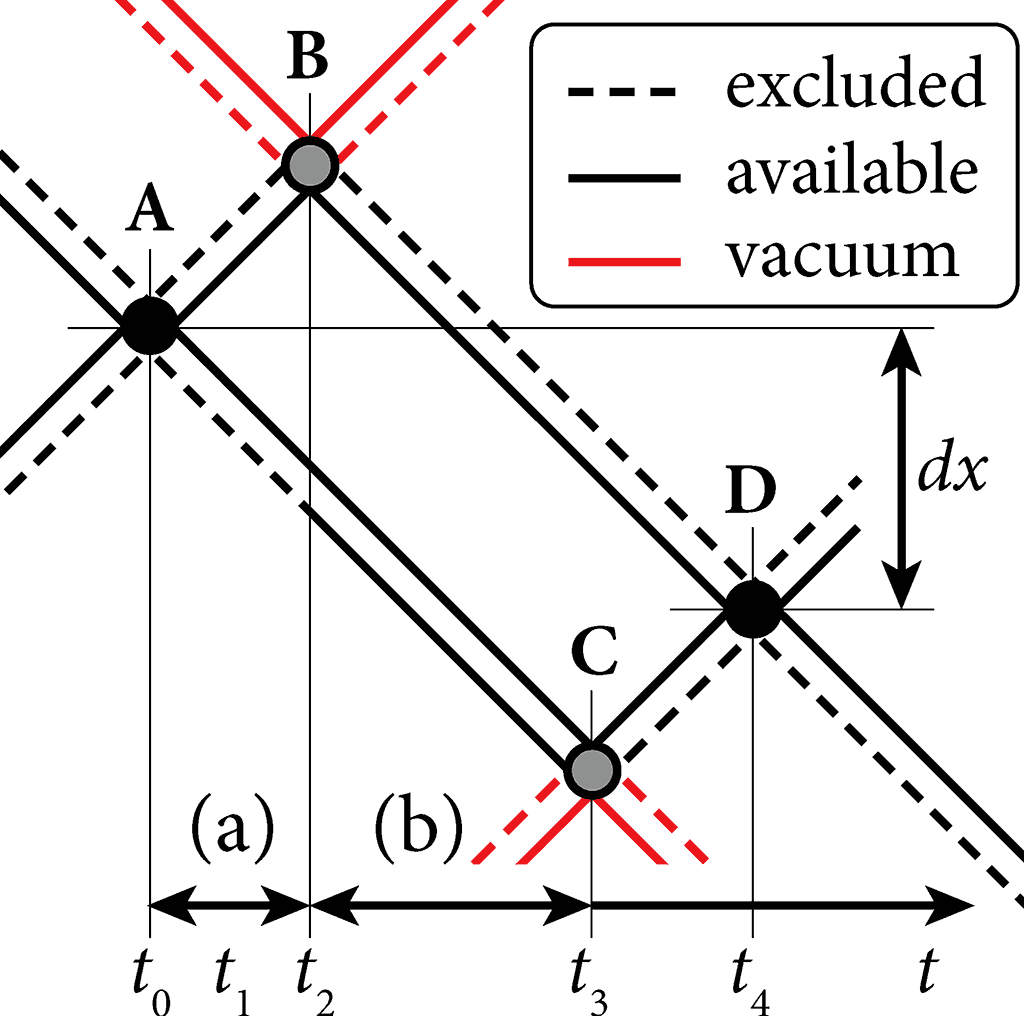
Fig.2: Re-constitution a fermion.
Disentanglement
The collapse of either boson, e.g. the collapse of boson AB at fermion event B, will break this entanglement and any associated symmetries. We propose this as the underlying mechanism for electro-weak symmetry-breaking.
The amplitude of boson AC doubles after B collapses, because both its waves are no longer excluded (fig.2: solid line), and are therefore free to collapse at a future event, e.g. fermion C. The addition of the other wave phase to the active wavefunction will enable a modulating phase operator of the opposite sign of its partner, enabling a 'phase window' in the opposite direction, equal in magnitude to the partner. This boson then becomes a superposition of two uncollapsed and available states, decided at event C.
Entanglement at larger scales
This entanglement can be expressed in larger-scale structures. For example, all the quarks are entangled with their siblings in a hadron: there is a persistent entanglement, even though it is constantly being broken, it is being re-encoded in further entanglements. The direction of a boson's angular momentum consistently correlates (or anti-correlates) with that of the other boson that left the fermion event. Indeed any two fermions that interact via bosons are each also involved in their own entanglement with another external entity.
It follows that all particles in the universe are entangled, but by varying degrees of separation and coherence (an indirect sequence of latent connections). This forms the basis of causality, which may be interpreted as a limited view on a predeterministic network, i.e. all events are fixed (in space, time), implying that all events predetermined, and our view of uncertain possible futures is merely the result of a lack of information about all states within the system.