Fermions have sub-parts?
In quantum mechanics we meet the notion of constitution: a preserved constitution is one where the particle under consideration remains the same: its intrinsic attributes and (if the particle can be reduced) its components are conserved throughout the operation, i.e. it is the same particle.
A consitution-invariant mechanism
At a fundamental level, our mechanism is the same regardless of the type of particle or field under examination. Whether you're looking at a fermion, a composite particle, bosons or radiation, vacuum flux, gravitation, magnetic flux, or degenerate matter, it all uses the same mechanism, without special variants for each type.
Encoding and reconstitution of matter
In the Physicality of Matter article, we describe how fermions may re-constitute from bosons. This structure for matter allows the constituent parts of a fermion to collapse independently to form fermion states with external bosons.
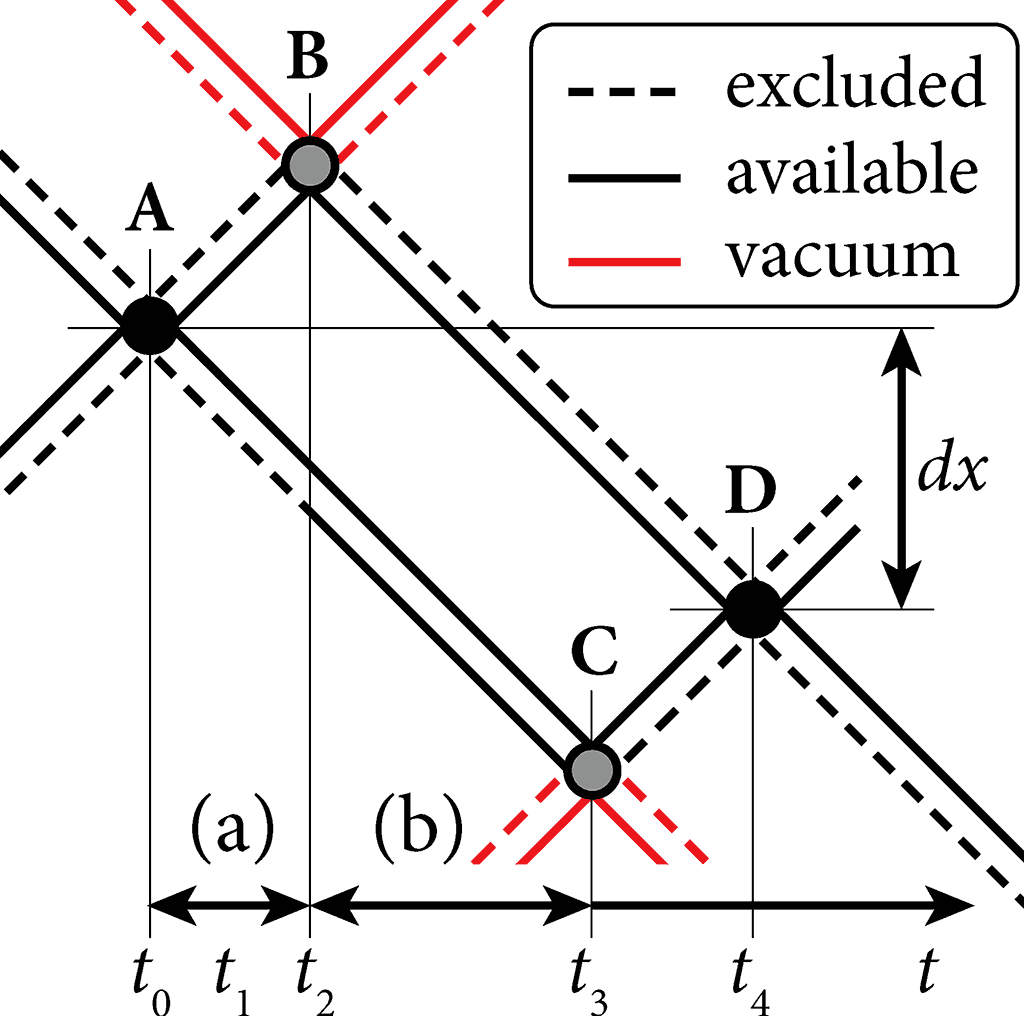
Fig.1: Conserved re-constitution of an electron-type fermion.
Particle decoherence
These fermions may then in turn re-radiate the same bosons back to the original fermion, or if that doesn't happen, then the two parts of the fermion will go their separate ways, having lost coherence (fig.2). They might never again reconstitute the original fermion, formed from the exact same instances of bosons. All fermions have the ability to change their constitution by having their own bosons substituted for bosons from elsewhere.
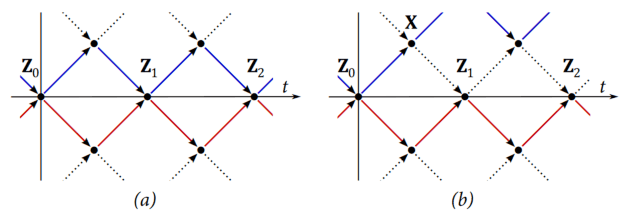
Fig.2: (a) Persistent Z state, and (b) a change of constitution.
This diagram is a simplification - we plan to update it shortly with a more detailed version.
The flux density of the environmental vacuum provides an 'external pressure' that is critical to the coherence of a particle. If it is rarefied, the vacuum-interacting bosons (fig.1: AB, AC) will propagate further before collapsing as anti-images (B,C).
This generalizes to a Compton radius, analytically found to have a 50th percentile radius for non-overlapping phases of a shell.
In the case of bound electrons, a rarefied vacuum flux makes them more susceptible to coupling with different baryonic structures, to create an ionized plasma or metallic material.
We can apply this coherence principle to all particles, and even black holes [15]
Decay
The introduction of overlapping bosons gives opportunities for the constitutional input required to create the extra fermions of standard weak decay modes:
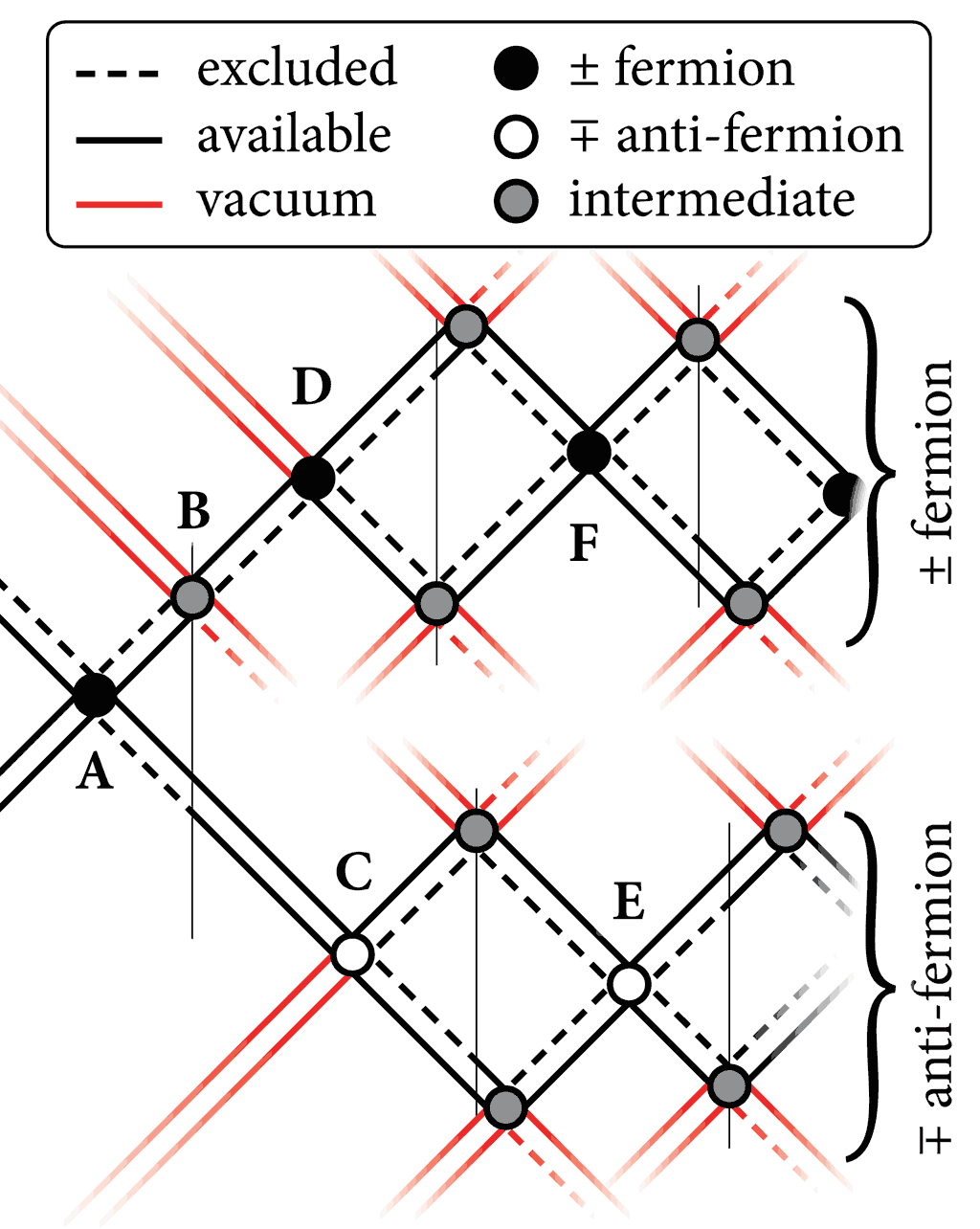
Fig.3: First decay products.
Axes: time →; compacted space ↕.
Fermion (D, F, …) and anti-fermion (C, E, …) are created from fermion A as it fails to reconstitute. Fermion B applies a weak symmetry break to the AC boson (AB and AC are entangled, from source A), and illustrates disturbance of the reconstitution sequence for an otherwise conserved fermion (fig.1).