We use a classical mechanism to constitute fermions from continuous waves, giving the quantum effects we expect, and a useful approach to the wave/particle duality.
See Physicality Described for a more readable introduction.
Basic phenomenology
Oscillators (bosons) and fermions are made of the same stuff, but their physical manifestation depends on the uniqueness of their attributes.
Oscillator
An oscillator is an entangled pairing of waves that encodes mass.
Fig.1: Oscillator propagation. See also: equivalence.
Boson shell
A boson is a propagating shell of oscillators that share the same spatial identity.
It exists as a degenerate entity, without unique location, and is disconnected from reality until it can form a fermion under the required conditions.
Fermion
A fermion is a point event where shells meet specific criteria. This generates discrete events from continuous waves.
Immediately after the event, all of its oscillators propagate on a new shell.
Fig.2: A fermion event, and its deconstitution.
Conserved constitution of fundamental particles
The same fundamental processes are at work for all entities, for accountable re-encoding of fermionic matter while conserving the oscillator information units.
A fermion is conserved when its constituents return to form another instance of the fermion.
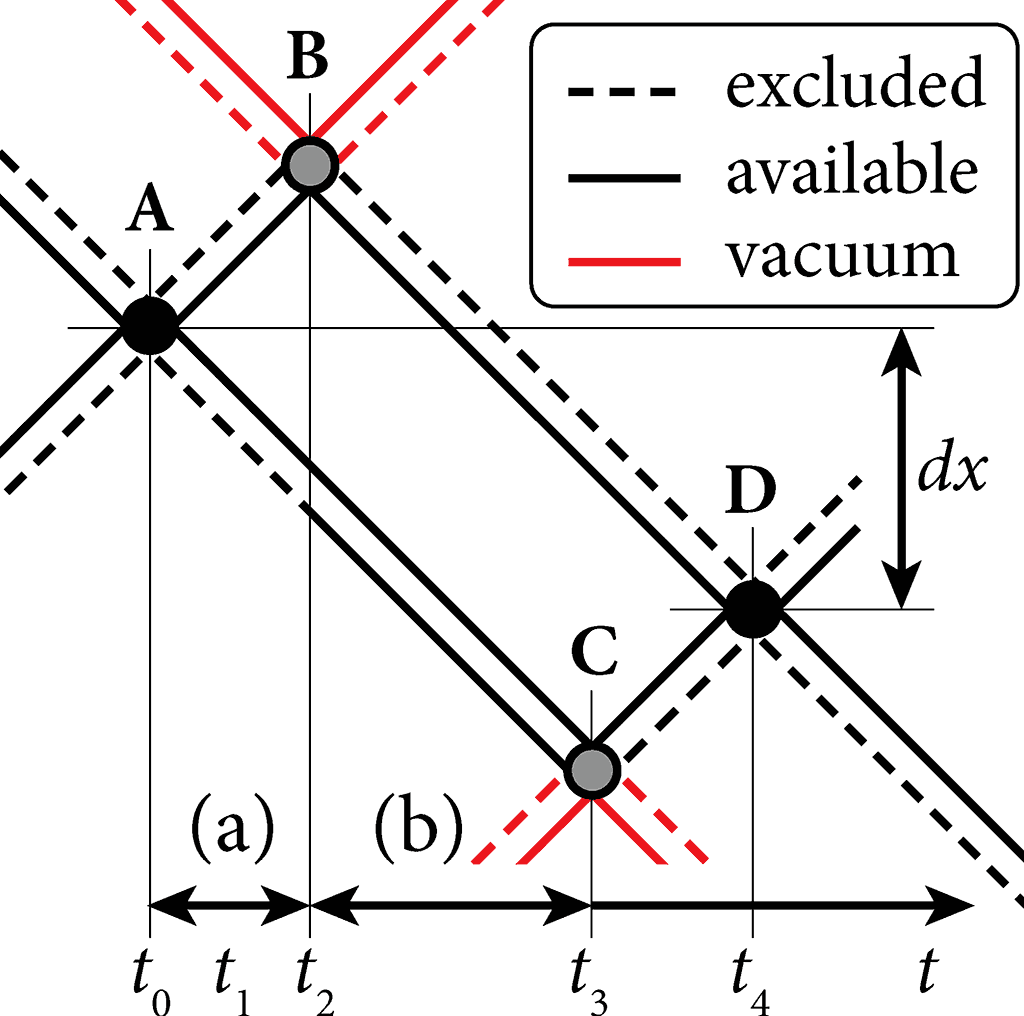
Fig.3: Conserved re-constitution
of an electron-type fermion.
In fig.3, the fermion A has two bosons which collapse by interacting with vacuum bosons at events B and C, which respectively radiate as bosons, and collapse at D. So, the fermion re-constituted at D, from A, with spatial displacement . The points A–D are the fermionic states of Zitterbewegung, with the vacuum interactions contributing a 'pressure' for the constitution, as found in the Casimir effect.
Classical velocity
The classical velocity for one conserved displacement is despite the constituent bosons propagating at light speed. More iterations may result in a respectively lower aggregated classical velocity, as vectors cancel out.
Matter networks
Each fermion has a minimum of two bosons entering the event, and two bosons leaving the event, forming a matter network when such bosons extend to other fermions on their world lines.
- A closed system is one where all bosons are connected to known fermions, and vice versa. A practical system is likely to be open, due to the nature of the vacuum.
- Persistent states are repeatedly re-constituted, and all fundamental bosons propagate at 'light speed'. Even classically stationary particles obey this rule; outgoing bosons form nearby fermions, and return as the same bosons.
- We regard the universe as a multitude of bosons, the fermions being the interaction events. Such a universe does not need a 'multiverse' to resolve quantum futures; quantum effects can be reconstructed without using contentious principles, and can be explained in terms of pairs of waves forming fermions.
- Quantum formulations and classical physics emerge naturally from the fundamental mechanics.
- Mass – Physical properties from the collapse function.
- Constitution – How a particle is conserved, and the exchange of bosons with vacuum.
The Standard Model
The three charge types are emergent properties of the mechanism, rather than abstractions. They have traceable origins in the collapse of waves, conservation of constitution, and exchange of waves with vacuum. Field and action effects emerge from the basic mechanics.
Gravitation emerges from the mechanism, without explicit encoding.
Electromagnetism
Magnetic currents emerge when vacuum waves interchange with fermion constituents, as charged interactions.
Photons are paired boson impulses, absorbed by structures like their emitters, having a frequency that may be derived from a sparse sampling of impulses
Photon emission
Weak interaction
The weak interaction is the change of potential when oscillators collapse from the shell, which happens for every fermion. The collapse of an oscillator might enable a remaining excluded wave on the shell to interact.
Strong force and quarks
Quarks and hadrons use oscillators with higher mass, in more confined networks. The generations are counts of oscillators collapsed at the fermion.
Higgs mechanism
A Goldstone boson is all waves output from a fermion. For example, for first-generation fermions, two of the four waves are non-excluded at any given time, until both its bosons are collapsed.
Our mechanism already has intrinsic mass generation at every fermion, and in propagated oscillators, so the Higgs functionality is already present, in a structure resembling the doublet of the scalar Higgs field.
Goldstone/Higgs boson
Gravitation
Gravitational interactions emerge from the collapse of a particles' own waves with those of the flux generated by 'classically organised' bodies. We are satisfied this is a unified mechanism.
Interpretations
General picture
Our interpretation of quantum mechanics is (pre)deterministic and Bohm-like, except we do not separate wavefunctions from instances; they are the same thing to us, dualled in ‘quanta’ oscillators that comprise the totality of the mass-energy.
The observer has limited knowledge of the matter network, resulting in a picture of probabilities for future collapses, which are realised regardless of observers.
Foundations and philosophy
In more abstract and philosophical terms, this mechanism can explain how many fermions may exist and couple. It was derived from the need to allow more than one entity to exist uniquely among others without ambiguity in resolving their differences.
Many important principles are intrinsic to the mechanism, which can be reconciled to its foundations and to high-level concepts in physics.